Moment of Inertia

Before I write this post on Moment of Inertia, I must admit, I have always been very poor at the subject. Even as an engineering student, the last subject I was ever interested in was SOM (Strength of Materials) or how most of us call it these days, Solid Mechanics. And ironically today I am writing a post on something from the same subject.

Anyways, coming back to the very much intended topic, what is moment of inertia? and how does it matter?

But before we jump on to Moment of Inertia, it will be wise to understand Inertia. In layman terms, inertia is nothing but resistance offered by a body to maintain its position/speed against an external force applied on it. Or say the tendency of a body to remain unchanged.

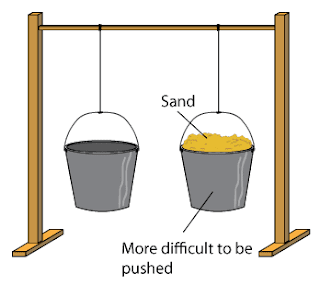
For instance, in the above picture, it is harder to push the bucket filled with sand compared to the empty one because it has got more mass. More mass means, its resistance to any external force is comparatively more, which means it has got more inertia, and that's all it is, or we can also look at it as an internal resistive force against an external force.

This is also covered by Newton's 2nd laws of motion, which says more or less the same thing, bigger is the mass, greater is the force required to move it.

  

Another very self explanatory example of Inertia

The above example not just sets another perfect explanation for inertia but on a different subject also tells us why proper load binding is so important on commercial vehicles and also how important the front wall design is on truck/trailer bodies. Anyways, now when we are clear about Inertia, lets look into Moment of Inertia. Like inertia is the resistance to an "linear" external force, Moment of inertia is the resistance offered by a body against an external rotational force applied on it about an axis and hence is also known as the rotational inertia.

By formula, Moment of inertia depends upon mass of the object and its distance from the rotational axis. More is the mass and farther it is from the rotational axis, more is the moment of inertia and hence more external force, or we can say more torque is required to move it.

But moment of inertia also depends on another factor, i.e. shape of the body or we can say, the way the mass is distributed. The shape of the body makes a big difference to the moment of inertia value. For instance, in the following picture, in both the cases, the mass of the person and the axis of rotation is the same, but in the first case, the mass is distributed away from the axis of rotation while in the second case, the mass is confined around the axis. Hence the moment of inertia is comparatively more in case one, and therefore more external force is required to rotate it.

Now, considering I have explained the term, I would like to clarify something here, as I have heard too many people misunderstanding it.

"Moment of inertia of a body doesn't tell us by itself how much load or force it can withstand, before it fails. It only tells us how much the body can resist the external force. Even by formula, we saw that it is a property of a body governed by its mass, shape and distance from the rotational axis. External loads are not used to calculate moment of inertia of any body."

Having said that, on the same time, it is useful when we calculate bending moments acting on a beam, which further tells us if the beam will be able to withstand the loads or not.

For instance, say I want to design a truck body and plan to design the base frame using I beams. Now, I don't want to use very heavy I beams, for it will reduce the payload capacity of the truck, hence, I need to know the exact size of the I beams I should go for, for the given pay load. Say I selected a 6"x8"x1" I beam. But the analysis tells me that the beams will fail against the given pay load. Which means, I need to go to a bigger I beam. But what size to go to? Say hypothetically, just for the sake of understanding the subject better, I instead of looking for another alternative or jumping to the next size of the I beam, I plan to get a custom I beam made to suit the application. But what should be the size? And that's where moment of inertia comes into the picture.

We can see from the above equation that Moment of Inertia of a body is inversely proportional to bending stress (acting on the body due to the external loads). So if we increase the moment of inertia of the beam, it further increases its load carrying capacity. Now where do we add more material?

 

As shown in the above picture, say I start by adding one square inch material to the I beam to have a better moment of inertia. As shown in the above picture, the first option gives me the greatest value, while adding the same amount of material somewhere else on the same beam gives comparatively poorer results. And hence, if an increase of 33.5% in the moment of inertia enables the beam to withstand the given loads, I would say I have got the optimum design solution.

Geometric Dimensioning & Tolerancing

Geometric Dimensioning & Tolerancing, commonly referred to as GD&T, as the name suggests, is a language used by design engineers to define/control and represent the "geometric shape" of a part/assembly on an engineering drawing. 

While, I am not very sure of the origin but I read somewhere that the initial idea was thrown around half a century ago. Today, GD&T is defined under various international standards, but the one followed the most is from American Society of Mechanical Engineers ASME Y14.5-2009.

As mentioned above, GD&T defines the shape of the product and not the size so it is not to be confused with the conventional dimensioning and tolerancing defining the size or features of a drawn part/assembly.


GD&T generally comes into picture where the shape of the part is of great importance to its application, for instance, the cylindricity of a piston inside an engine cylinder. If the piston is not cylindrical, the engine won't be efficient for the obvious reason.

Having said that, how do we use GD&T on the drawings. GD&T has its own set of symbols and modifiers used to define the geometry of a part. While the symbols define the kind of tolerance being applied, modifiers defines the material conditions. 

The symbols are divided under five categories, as shown below.

Generally, the geometry is defined with respect to a defined set of datum/datums. The only exception is the "Form" category, which do not needs a datum to define the geometry of the given part. For instance, the flatness tolerance in the following example, doesn't need a datum to define it against.

Flatness

While other tolerances, for instance perpendicularity in the following example, needs a datum plane A to hold the perpendicularity against. Generally the assumption with datums is that the datum is x10 times precise than the plane given the tolerance.

Perpendicularity

Runout (also called circular runout)/Total Runout comes into the picture when we plan to control the wobbling of a shaft (hollow/solid) around its center axis. Its measured against the central axis (considered as the datum) using a Full Indicator Movement (FIM) gauge. So as shown in the picture below, the shaft is rotated around its axis and the variance of 0.1mm is measured with FIM. And as the variance is within 0.1mm, the part is good to go.

Total Runout

Now what are modifiers? Modifiers as mentioned above defines the material condition of the part, the tolerance is applied on. 

For instance, when MMC (Max Material Condition) is applied to a Ø10±.5mm hole, it will have the smallest diameter Ø9.5mm. While the same hole at LMC (Least Material Condition), would have the largest diameter Ø10.5mm.

On the same time, if the same conditions are applied on a pin/shaft of diameter Ø10±.5mm, the pin will have the largest diameter at MMC i.e. Ø10.5mm and the smallest diameter at LMC i.e. Ø9.5mm.

This is very handy when it comes to Gauges used by Quality Engineers on the floor to measure a part. A gauge set to MMC/LMC depending on the functionality of the part is all that would be required for the quality check. 

 


Now how do we use them to define the geometry of a part on the drawings? GD&T is defined inside what is called "Feature Control Frame"

 

In the above example, lets assume that GD&T is applied to a hole (and not a pin) with a diameter range of Ø.505-.525in with a positional tolerance of .005 at Max Material Condition, with respect to the primary datum A, the secondary datum D (again at max material condition) and then the tertiary datum B. 

So this means that the positional tolerance of .005in is applied on the hole at Ø.505in (@MMC) against the given datums.

Simplifying it further, the hole will have a positional tolerance between .500 - .510mm, or in technical terms will have an envelop of .500 - .510mm.

There are a lot of opinions people have when it comes to GD&T, like it increases the cost or is difficult to go about and what not. But as per my understanding, it is not that difficult to go about once you get your head around it and as far as the cost is concerned, GD&T is all about manufacturing a product within the right functional tolerances which further leads to low rejection rate and ends up saving the cost.

In this post I have tried to give out a rough idea of what GD&T is and how its being used. I used it in one of my previous roles where I was involved in the design and development of precise plastic components with close tolerances but not in my present role, so while writing this post, I could feel a lot of it coming back to my mind. I won't probably dig any further into the subject as its gonna be then a never ending post. But will be glad if it gives you the basic intended idea.